PriMa: Uni-Zirkel Klasse 3/4

Hintergrundinformationen zu den PriMa -Uni- Zirkeln

Seit dem Schuljahr 1999/2000 fördern wir im Rahmen der PriMa-Maßnahme mathematisch besonders begabte Dritt- und Viertklässler an der Universität (Uni-Zirkel). Nach einer Talentsuche erhalten alle Kinder, die daran bis zum Ende teilnehmen, ein Förderangebot. Etwa fünfzig Kinder pro Jahrgang können an der Universität gefördert werden, die anderen Kinder erhalten das Angebot, an (Schul-) Mathe-Zirkeln, die an verschiedenen Grundschulen angeboten werden, teilzunehmen.

An der Universität werden Kinder gefördert, deren Fähigkeiten bezogen auf mathematische Inhalte durch eine beeindruckende Schnelligkeit im Problemlösen und die Fähigkeit sich rasch in sehr komplexe Problemfelder einzudenken gekennzeichnet sind. In einer Gruppe vergleichbar begabter Kinder werden damit neben der Weiterentwicklung ihrer kognitiven Kompetenzen insbesondere ihre Kommunikationsfähigkeit, ihre Belastbarkeit und ihre Anstrengungsbereitschaft entwickelt.

Ein spezielles Angebot für Mathematik kommt insbesondere den Kindern entgegen, die eine sehr hohe mathematische Begabung bei gleichzeitig “nur” überdurchschnittlichen oder “nur” weit überdurchschnittlichen Begabung in anderen Bereichen zeigen.

Wir fördern an der Universität pro Jahrgang etwa 45 – 50 Kinder. Die Förderung erstreckt sich vom Ende der Talentsuche von ca. Mitte der dritten bis Ende der vierten Klasse.

Die Kinder treffen sich etwa zweiwöchentlich freitagnachmittags an der Universität. Dort arbeiten wir mit ihnen in mehreren Gruppen meistens ungefähr 90 Minuten (16.00-17.30 Uhr), zu besonderen Anlässen auch bis zu zwei Zeitstunden. Neben der Talentsuche bieten wir so für die Kinder etwa 19 Fördersitzungen an. Pro Sitzung, manchmal auch über zwei Sitzungen, wird eine Aufgabe bearbeitet.

Zum konzeptionellen Ansatz der Förderung

Das Projekt ist als Enrichment-Programm angelegt. Es werden in der Regel keine Inhalte der zukünftigen Schuljahre angesprochen. Wir konzipieren für Schülerinnen und Schüler mit besonderen mathematischen Begabungen Lernumgebungen so, dass eine möglichst viele gute Ideen auslösende und zu ausdauernder Beschäftigung motivierende Gesamtkonstellation geschaffen wird, in der sich die Kinder wohl fühlen sollen. Das bezieht sich auf die Entwicklung von Aufgabenstellungen (Progressive Forscheraufgaben), auf methodische Fragen und auf das Umgehen miteinander, sowie mit Erfolgen und Misserfolgen.

Progressive Forscheraufgaben (ProFa)

Die Kinder erhalten Aufgaben, die selbstdifferenzierend sind. Die Aufgaben sollen herausfordernd sein, aber nur klassenstufen angemessene Vorkenntnisse erfordern. Sie sollen hinreichend komplex sein, um verschiedene Vorgehensweisen bei der Bearbeitung zu ermöglichen. Sie sollen mehrere Fragestellungen zulassen und auf verschiedenen Niveaus zu bearbeiten sein. Dies wird auch dadurch begünstigt, dass unterschiedlich weit in die mathematischen Fragestellungen eingedrungen werden kann. Damit eignen sich die meisten Aufgaben sowohl für einen Einsatz in Regelklassen als auch in Gruppen von besonders begabten Kindern, natürlich mit unterschiedlicher Bearbeitungstiefe. Wir nennen unsere Aufgaben Progressive Forscheraufgaben (ProFa), da sie propädeutisches forschendes Lernen ermöglichen. Die Beschäftigung mit den ProFa ermöglicht es, Lernprozesse zu initiieren, die den zukünftigen Tätigkeiten des mathematischen Forschens ähneln.

ProFa sind so gestaltet, dass sie von einer Einstiegsfrage ausgehend weitere Fragen zum Bearbeiten bieten und damit ein Problemfeld eröffnen. Diese Art des Weiterdenkens und Weiterfragens zu entwickeln gehört zum Ansatz unseres Projekts. Den Kindern werden damit erste Erfahrungen in komplexen mathematischen Problemfeldern ermöglicht.

Methodische Überlegungen
Arbeiten in komplexen Problemfeldern erfordert nicht nur ein Umgehen können mit größerer Komplexität, sondern auch besondere Ausdauer.

Für die Entwicklung eines angemessenen Durchhaltevermögens ist es wichtig, dass die Kinder rasch erste Erfolge erzielen können und immer wieder Zwischenerfolge möglich sind. Die Aufgabenstellung und deren Bearbeitung sind um ein Vielfaches länger als das, was die Kinder aus der Schule gewohnt sind.  Hier orientieren wir uns an dem Kießwetter’schen Ansatz, der davon ausgeht, dass über eine Anfangsmotivation hinausgehend die Prozessmotivation entscheidend für die Fähigkeit ist, über einen längeren Zeitraum an mathematischen Fragen zu arbeiten. Insbesondere die Ausdauer im Prozess der Bearbeitung soll durch Zwischenerfolge ermöglicht werden.

Für Kinder dieser Altersstufe muss eine Balance hergestellt werden zwischen Selbstständigkeit und Anleitung. Forschendes Lernen erfordert zwingend individuelle Vorgehensweisen und eigene Fragestellungen zu ermöglichen. In der Altersgruppe der Grundschulkinder sind jedoch noch zu wenige Erfahrungen im Umgang mit herausfordernden Problemstellungen verfügbar. Weiterhin sollen Fragen, die sich im Problemlöseprozess ergeben oder darin anschließen zu substanziellen mathematischen Überlegungen führen.

Unter der Leitung von Prof. Dr. M. Nolte entstand im Verlauf des Grundschulprojekts an der Universität Hamburg der  folgender Ansatz: Die Kinder werden zunächst insbesondere zu Beginn der Förderung  genau angeleitet, um sie eng zum mathematischen Kern einer Fragestellung zu führen. Dies hat den Zweck sicherzustellen, dass das Ausgangsproblem verstanden wurde. Wir vermeiden es, sie mit einem für sie noch ungeordneten Problemfeld allein zu lassen, damit ihnen genügend Kapazität zur Verfügung steht, sich im Folgenden mit sehr komplexen Strukturen und Fragestellungen zu befassen. Deshalb vermeiden wir ein eigenständiges Entdecken von Eingangsfragen bewusst. Erst zum Ende der Förderung werden die Kinder angeregt, schon zu Beginn der Sitzung selbst Fragen an das Material zu stellen. Die Kinder beginnen zunächst an einer bestimmten vorgegebenen Fragestellung. Diese kann jedoch auf verschiedene Weise bearbeitet werden und ermöglicht in dem komplexen Problemfeld, dass Kinder verschiedene Aspekte entdecken und verschiedene Gedanken weiter verfolgen. An dieser  Stelle sind eigene und unterschiedliche Fragestellungen nicht nur erlaubt, sondern auch erwünscht. Das bedeutet, dass die enge Führung der Kinder durch die Präsentation an einem bestimmten Punkt wieder verlassen wird und eine breite Vielfalt an Vorgehensweisen und Gedanken, die weiterverfolgt werden können, ermöglicht wird:

 

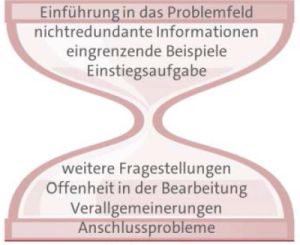
Die Lenkung in der ersten Phase soll sicherstellen, dass sich die Kinder nicht im Erschließen des Problems verausgaben. Die einführende Teil-Aufgabe soll rasch zu Erfolgen führen und gleichzeitig das Verständnis des Problems vertiefen. Damit soll den Beschränkungen des Arbeitsgedächtnisses sowie der noch geringen Belastbarkeit der Kinder entsprochen werden. Daran anschließend werden weitere Hinweise gegeben. In der Regel findet an dieser Stelle ein Zwischenplenum statt. Hier werden die unterschiedlichen Ergebnisse und Vorgehensweisen zusammengetragen. Ein bestimmtes Niveau an Erkenntnissen wird dadurch allen Kindern angeboten. Daran anschließende weiterführende Fragestellungen sind generell offen bezüglich der Bearbeitung. Sie können zu unterschiedlichen Anschlussproblemen führen.

Die von uns eingesetzten Problemstellungen sind teilweise der Literatur entnommen und werden für unsere Vorstellungen modifiziert. Teilweise sind es eigene Entwicklungen. Zu Beginn unserer Arbeit stammten entscheidende Anregungen für die Konzeption unserer Materialien von Herrn Prof. Dr. Karl Kießwetter. Regelmäßig werden die ProFa mit den Mitarbeiterinnen und Mitarbeitern des Projekts weiterentwickelt.